

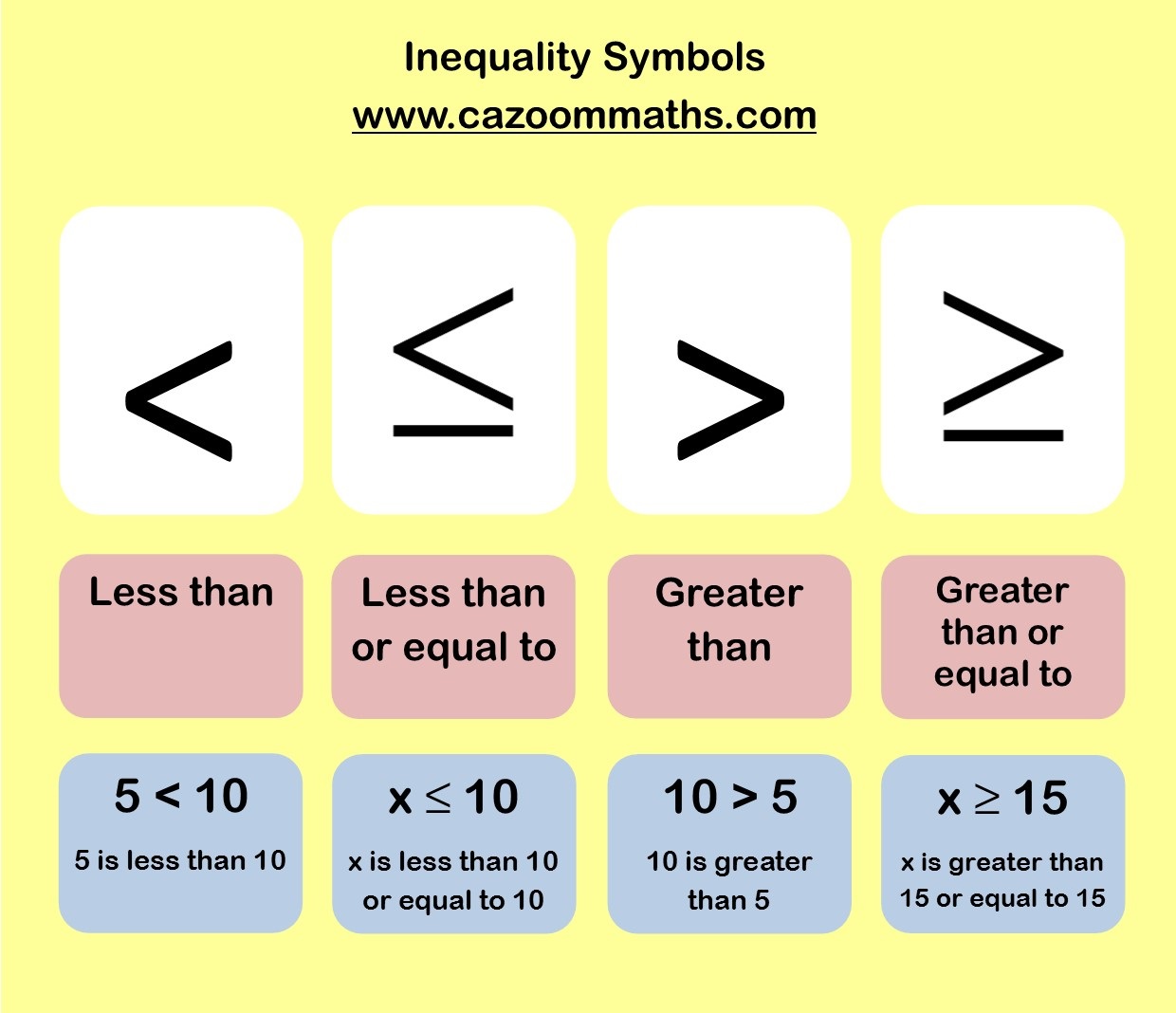
However, applying a monotonically decreasing function to both sides of an inequality means the inequality relation would be reversed. The relations ≤ and ≥ are each other's converse, meaning that for any real numbers a and b:Īny monotonically increasing function, by its definition, may be applied to both sides of an inequality without breaking the inequality relation (provided that both expressions are in the domain of that function). All of these properties also hold if all of the non-strict inequalities (≤ and ≥) are replaced by their corresponding strict inequalities () and - in the case of applying a function - monotonic functions are limited to strictly monotonic functions. Inequalities are governed by the following properties. 2 Formal definitions and generalizations.In all of the cases above, any two symbols mirroring each other are symmetrical a a are equivalent, etc.
This implies that the lesser value can be neglected with little effect on the accuracy of an approximation (such as the case of ultrarelativistic limit in physics). The notation a ≫ b means that a is much greater than b.The notation a ≪ b means that a is much less than b.
In engineering sciences, less formal use of the notation is to state that one quantity is "much greater" than another, normally by several orders of magnitude. It does not say that one is greater than the other it does not even require a and b to be member of an ordered set. The notation a ≠ b means that a is not equal to b this inequation sometimes is considered a form of strict inequality. The same is true for not less than and a ≮ b. The relation not greater than can also be represented by a ≯ b, the symbol for "greater than" bisected by a slash, "not".


 0 kommentar(er)
0 kommentar(er)
